ETOPO1で地球全体の高度段彩図と陰影起伏図から、陰影段彩図を作成してみる
前回、ETOPO1の地球全体の標高・水深データを使い、地球の各地点の標高・水深の高さ、および深さ1m毎に別の色で色付けして地図を作ってみましたが、
このような標高値を高度の段階ごとに分け、その段階ごとに色付けした地図を高度段彩図と呼ぶそうで、それに、陰影起伏図を重ねて立体感を出したものを陰影段彩図と呼ぶとのことで、早速作ってみることに。

ETOPO1グローバル地形データセット
https://www.ngdc.noaa.gov/mgg/global/global.html
の説明は以下を参照して頂くとして
前回、標高値をその段階ごとに色付けした高度段彩図を作成するのに、matplotlibのpcolor関数を使い、matplotlibの描画領域に標高値に応じた色をpcolor関数で塗りつぶすという形で高度段彩図を作成しましたが、
ETOPO1に掲載の地図のような、緯緯度が方眼紙状に直角かつ等間隔にマッピングした正距円筒図法(plate carrée)として地図画像を出力するだけなら、考えてみたら、matplotlibの描画機能や地図ライブラリーは使用する必要はなく、単に、標高値の入った配列の各ピクセルを、標高に応じた色に置換するだけの単純作業じゃんとはたと思い至り
numpyの配列操作だけで地球全体の高度段彩図を作成してみたのが以下で

ソースは単純にこれだけで
上の高度段彩図は描けてしまいます
#!/usr/bin/env python # -*- coding: utf-8 -*- from netCDF4 import Dataset import numpy as np import matplotlib.colors as colors from matplotlib import cm from sklearn import preprocessing from scipy import misc def makecolormap(): # 基点となる標高での色を配列として定義する color = np.array([[-12000, 'darkblue'], [-6000, '#0938BF'], [-2500, '#50D9FB'], [-1, '#B7E5FA'], [0, '#1F4806'], [100, '#68E36B'], [150, '#98D685'], [300, '#F9EFCD'], [800, '#E0BB7D'], [1000, '#D3A62D'], [2500, '#997618'], [3000, '#705B10'], [3500, '#5F510D'], [4000, '#A56453'], [5000, '#5C1D09'], [5500, 'snow'], [12000, 'white']]) # 標高値を0..1の範囲に正規化 hight = color[:, 0].astype(np.float32) hightnorm = preprocessing.minmax_scale(hight) # 正規化した標高値と各色の組みのリストcolornormを生成 colornorm = [] for no, norm in enumerate(hightnorm): colornorm.append([norm, color[no, 1]]) # colornormに従いグラデーションカラーマップを作成 cmap = colors.LinearSegmentedColormap.from_list('a', colornorm, N=hight.max()-hight.min()+1) # カラーマップを割り当てる1m間隔の標高値 hightbounds = range(int(hight.min()), int(hight.max()+1)) return cmap, hightbounds # ETOPO1を読み込む etopo1 = Dataset('ETOPO1_Bed_g_gmt4.grd','r') # 標高・水深データを読み込む Z=etopo1.variables['z'][:] # 地球全体を一気に描くにはデーターがでかいのでメッシュを4分の1に間引く Z=Z[::4,::4] # 標高値の配列は南北逆なので逆順にする Z = Z[::-1] # -12000m〜12000mまでのカラーグラデーションを作成する cmap, hightbounds = makecolormap() # 標高・水深に応じたカラーイメージ配列を生成する # カラーグラデーションの+12000が0mに対応するので標高値は+12000する img =cmap(Z+12000) # 透過情報はカット img=img[:,:,:3] # scipyのmisc関数でカラーイメージを書き出す img*=255 img = np.uint8(img) misc.imsave('1.jpg', img)
で、それにそれに、
ある方向から光を当てたときに地表面に生じる陰影を再現した陰影起伏図を作成し

ソースは以下
#!/usr/bin/env python # -*- coding: utf-8 -*- from netCDF4 import Dataset import numpy as np import matplotlib.colors as colors from matplotlib import cm from sklearn import preprocessing from scipy import misc # 指定緯度帯のZ係数を返す def Z_factor(lat): zfactors = { 0 : 0.00000898, 10 : 0.00000912, 20 : 0.00000956, 30 : 0.00001036, 40 : 0.00001171, 50 : 0.00001395, 60 : 0.00001792, 70 : 0.00002619, 80 : 0.00005156 } return zfactors[np.trunc(lat/10.0)*10.0] # 標高値から陰影起伏 (Hillshade) を計算する def hillshade(Z, center_Lat, azimuth_deg, altitude_deg): # 通常の陰影起伏図は、光源方位 315 度、光源方位 45 度で描画 # # 陰影起伏 = 255.0 * ((cos(Zenith_rad) * cos(Slope_rad)) + # (sin(Zenith_rad) * sin(Slope_rad) * cos(Azimuth_rad - Aspect_rad))) # 勾配(傾き)を求める Zy, Zx = np.gradient(Z) # 傾斜角 Slope_rad = np.arctan(30 * Z_factor(center_Lat) * np.sqrt(Zx*Zx + Zy*Zy)) # 傾斜方向 Aspect_rad = np.arctan2(-Zx, Zy) # 太陽の方位角をラジアンに変換 Azimuth_rad = np.radians(360.0 - azimuth_deg + 90) # 太陽の天頂角をラジアンに変換 Zenith_rad = np.radians(90 - altitude_deg) # 陰影起伏 shaded = np.cos(Zenith_rad) * np.cos(Slope_rad) + np.sin(Zenith_rad) * np.sin(Slope_rad) * np.cos(Azimuth_rad - Aspect_rad) return 255 * shaded # 画像を平坦化する def imgFlattening(img): # 画像のヒストグラムを平坦化する # ヒストグラムを取得 hist, bins = np.histogram( img.flatten(), bins=256 ) # 累積分布を取る cdf = hist.cumsum() # 0〜255の範囲に正規化 cdf = 255 * cdf / cdf[-1] # ヒストグラムが平坦化するよう線形補間 img2 = np.interp( img.flatten(), bins[:-1], cdf) return img2.reshape( img.shape ) # ETOPO1を読み込む etopo1 = Dataset('ETOPO1_Bed_g_gmt4.grd','r') # 標高・水深データを読み込む Z=etopo1.variables['z'][:] # 地球全体を一気に描くにはデーターがでかいのでメッシュを4分の1に間引く Z=Z[::4,::4] # 標高値の配列は南北逆なので逆順にする Z = Z[::-1] # 標高タイルから陰影起伏を計算する Zshade = hillshade(Z, 0, 315, 60) # 陰影起伏を0..1に正規化 Zshade_norm = (Zshade-Zshade.min())/(Zshade.max()-Zshade.min()) # 陰影起伏をグレイスケール画像にする projectionIMG = cm.binary(Zshade_norm)*255 # 透過情報はカット projectionIMG = projectionIMG[:,:,:3] # 陰影起伏図の画像を平坦化して明度のバランスを整える projectionIMG = imgFlattening(projectionIMG) # scipyのmisc関数でカラーイメージを書き出す projectionIMG = np.uint8(projectionIMG) misc.imsave('1.jpg', projectionIMG)
高度段彩図と陰影起伏図を合成すれば陰影段彩図なりますねということで、画像を合成してみたのが以下になります。

ソースは以下
#!/usr/bin/env python # -*- coding: utf-8 -*- from netCDF4 import Dataset import numpy as np import matplotlib.colors as colors from matplotlib import cm from sklearn import preprocessing from scipy import misc def makecolormap(): # 基点となる標高での色を配列として定義する color = np.array([[-12000, 'darkblue'], [-6000, '#0938BF'], [-2500, '#50D9FB'], [-1, '#B7E5FA'], [0, '#1F4806'], [100, '#68E36B'], [150, '#98D685'], [300, '#F9EFCD'], [800, '#E0BB7D'], [1000, '#D3A62D'], [2500, '#997618'], [3000, '#705B10'], [3500, '#5F510D'], [4000, '#A56453'], [5000, '#5C1D09'], [5500, 'snow'], [12000, 'white']]) # 標高値を0..1の範囲に正規化 hight = color[:, 0].astype(np.float32) hightnorm = preprocessing.minmax_scale(hight) # 正規化した標高値と各色の組みのリストcolornormを生成 colornorm = [] for no, norm in enumerate(hightnorm): colornorm.append([norm, color[no, 1]]) # colornormに従いグラデーションカラーマップを作成 cmap = colors.LinearSegmentedColormap.from_list('a', colornorm, N=hight.max()-hight.min()+1) # カラーマップを割り当てる1m間隔の標高値 hightbounds = range(int(hight.min()), int(hight.max()+1)) return cmap, hightbounds # 指定緯度帯のZ係数を返す def Z_factor(lat): zfactors = { 0 : 0.00000898, 10 : 0.00000912, 20 : 0.00000956, 30 : 0.00001036, 40 : 0.00001171, 50 : 0.00001395, 60 : 0.00001792, 70 : 0.00002619, 80 : 0.00005156 } return zfactors[np.trunc(lat/10.0)*10.0] # 標高値から陰影起伏 (Hillshade) を計算する def hillshade(Z, center_Lat, azimuth_deg, altitude_deg): # 通常の陰影起伏図は、光源方位 315 度、光源方位 45 度で描画 # # 陰影起伏 = 255.0 * ((cos(Zenith_rad) * cos(Slope_rad)) + # (sin(Zenith_rad) * sin(Slope_rad) * cos(Azimuth_rad - Aspect_rad))) # 勾配(傾き)を求める Zy, Zx = np.gradient(Z) # 傾斜角 Slope_rad = np.arctan(30 * Z_factor(center_Lat) * np.sqrt(Zx*Zx + Zy*Zy)) # 傾斜方向 Aspect_rad = np.arctan2(-Zx, Zy) # 太陽の方位角をラジアンに変換 Azimuth_rad = np.radians(360.0 - azimuth_deg + 90) # 太陽の天頂角をラジアンに変換 Zenith_rad = np.radians(90 - altitude_deg) # 陰影起伏 shaded = np.cos(Zenith_rad) * np.cos(Slope_rad) + np.sin(Zenith_rad) * np.sin(Slope_rad) * np.cos(Azimuth_rad - Aspect_rad) return 255 * shaded # 画像を平坦化する def imgFlattening(img): # 画像のヒストグラムを平坦化する # ヒストグラムを取得 hist, bins = np.histogram( img.flatten(), bins=256 ) # 累積分布を取る cdf = hist.cumsum() # 0〜255の範囲に正規化 cdf = 255 * cdf / cdf[-1] # ヒストグラムが平坦化するよう線形補間 img2 = np.interp( img.flatten(), bins[:-1], cdf) return img2.reshape( img.shape ) # ETOPO1を読み込む etopo1 = Dataset('ETOPO1_Bed_g_gmt4.grd','r') # 標高・水深データを読み込む Z=etopo1.variables['z'][:] # 地球全体を一気に描くにはデーターがでかいのでメッシュを4分の1に間引く Z=Z[::4,::4] # 標高値の配列は南北逆なので逆順にする Z = Z[::-1] # -12000m〜12000mまでのカラーグラデーションを作成する cmap, hightbounds = makecolormap() # 高度段彩図を作成する img =cmap(Z+12000) # 透過情報はカット img=img[:,:,:3] img*=255 # 標高値から陰影起伏を計算する Zshade = hillshade(Z, 0, 315, 60) # 陰影起伏を0..1に正規化 Zshade_norm = (Zshade-Zshade.min())/(Zshade.max()-Zshade.min()) # 陰影起伏をグレイスケール画像にする projectionIMG = cm.binary(Zshade_norm)*255 # 透過情報はカット projectionIMG = projectionIMG[:,:,:3] # 陰影起伏図の画像を平坦化して明度のバランスを整える projectionIMG = imgFlattening(projectionIMG) # 高度段彩図と射影陰影図を足して2で割りゃ画像が合成される img = (img + projectionIMG) / 2.0 # 合成画像を平坦化してサイド明度のバランスを整える img = imgFlattening(img) # 陰影段彩図を出力する img = np.uint8(img) misc.imsave('1.jpg', img)
なお、上のソースで描いたETOPO1の4分の1のメッシュで描いた画像の実際のサイズは以下になります
https://cdn-ak.f.st-hatena.com/images/fotolife/m/memomemokun/20190303/20190303220818.jpg
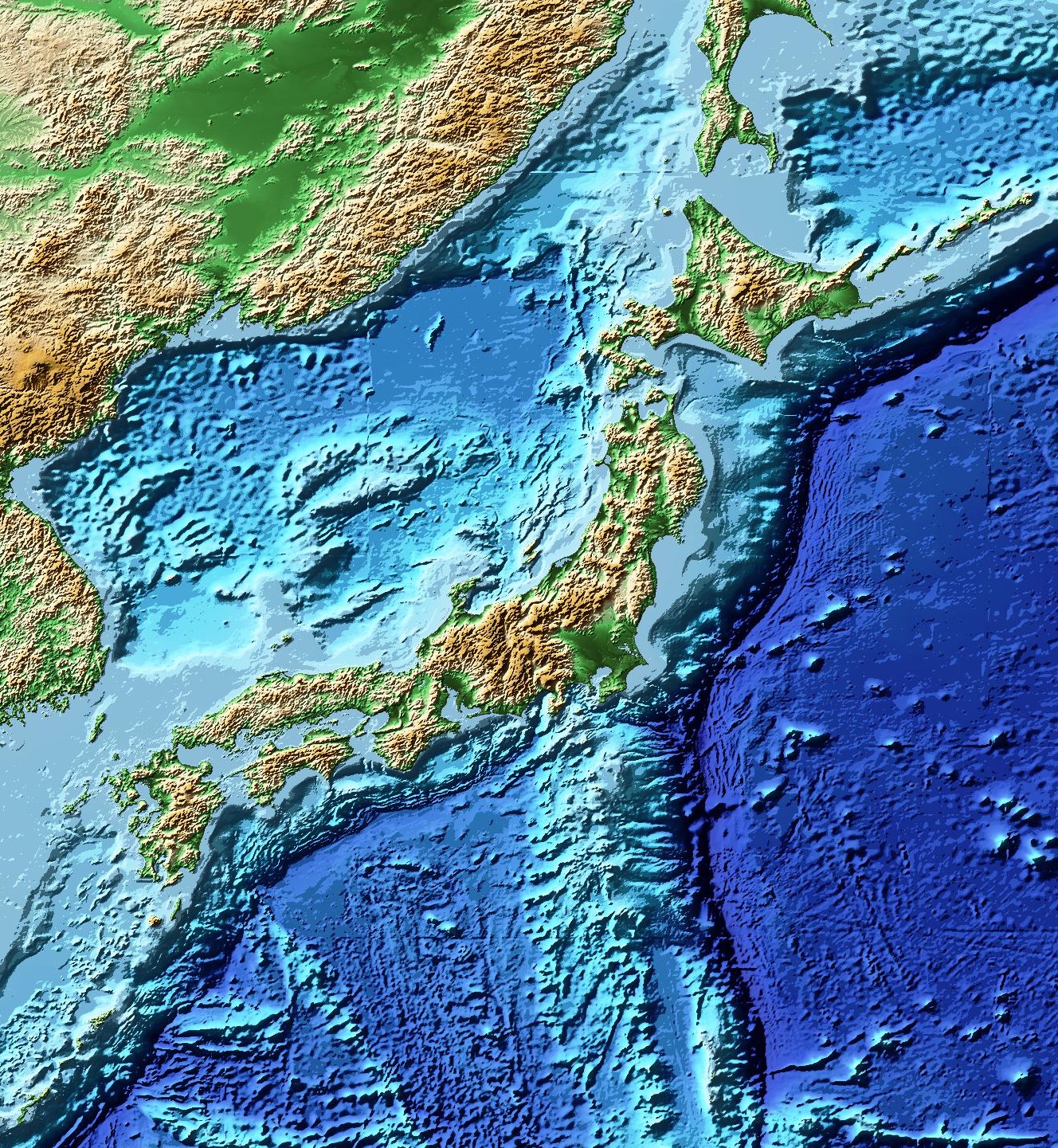
また、ETOPO1のメッシュフルサイズで日本近辺の陰影段彩図を描いてみるとこんな感じの解像度になります。(画像を別ウインドウで開くと実際のサイズが確認できます)