プログラム日記φ(．．)

おもにPython関係のプログラムメモ

トップ > Python > 富士山の法線マップをPythonで作ってみる。

富士山の法線マップをPythonで作ってみる。

Python X3D 地図作成

X3DOMでグリグリ動く3D世界地図用の法線マップを作ってみようということで

  

memomemokun.hateblo.jp

 

 

先日、地球観測衛星「だいち」の標高モデルで立体富士山を描いたときに利用した

 

memomemokun.hateblo.jp

 

 

宇宙航空研究開発機構（JAXA）の陸域観測技術衛星「だいち」（ALOS）による、30mメッシュの標高データ「ALOS全球数値地表モデル(DSM) "ALOS World 3D - 30m (AW3D30)"」を使い、富士山周辺の法線マップ（normal mapping）を作ってみました。

 

で、法線マップってなに？

 

と、調べてみると、初心者の特権で簡略に要約させていただければ、そんなに難しいことを言ってるわけではなく、単に、物体の表面上の各点に垂直な方向はどの方向かという情報を画像のRGB値に変換して画像として保存したものと要約しちゃっていいんじゃないかと思うんですけど。

 

で、空間内の方向というのは、ベクトルとして、各XYZ軸方向の大きさがわかれば一意に定まりますので、対象とする図形の表面に垂直なベクトルのXYZ軸方向の成分をRGB値に変換して保存した画像が法線マップということになります。

 

と、いうことは、地図上の情報なら斜面の各ポイントごとの垂直方向を導ければ、あとはデータの変換だけの問題で、じゃ、どうやって、斜面に垂直な方向を導くのということですが、

 

図形の表面がなんらかの方程式で与えられている単純な場合はその曲面の方程式から偏微分などを使って直接法線方向を求めればその値は得られますが、自然の山の地形など、世の中に散らばる自然の造形物の場合は、その表面を表す簡単な方程式があるわけでもなく、

 

幸い、地図上の標高データや画像のピクセルデータなどの一般のデジタルデータの場合は、一般に縦横に格子状のデータとしてなんらかの大きさを表す値が提供されてますので、ここで、ちょっと妥協しまして、

 

地図上の標高データの縦横隣同士の標高差を求めれば平均斜度が求まりますので－－なお、下のソースのnp.gradient函数の場合は、隣の点との標高差というより、対象とする点を中心とした前後２つの区画の平均斜度として値が求まります－－それを利用すれば大雑把な法線方向はわかるんじゃないのと割り切ってしまえば、ここからは、高校の数学の問題で、横方向に隣同士の点の高さの差はそれぞれの差として簡単に求まりますので、X方向の隣の点までの高低差のベクトルがわかります。

 

同様に、Y方向の隣の点までの高低差のベクトルもわかりますので、各点に２方向のベクトルが与えられれば各点を通り２つのベクトルを含む平面は一意に定まるというのも高校で習いましたので、それを、大雑把に、各点の斜面と考えれば、その平面に垂直なベクトルは２つのベクトルが作る平行四辺形の面積と等しい大きさを持った、平面に垂直なベクトルとして、こちらも、高校で習ったベクトルの外積（クロス積）として求まりますので、

 

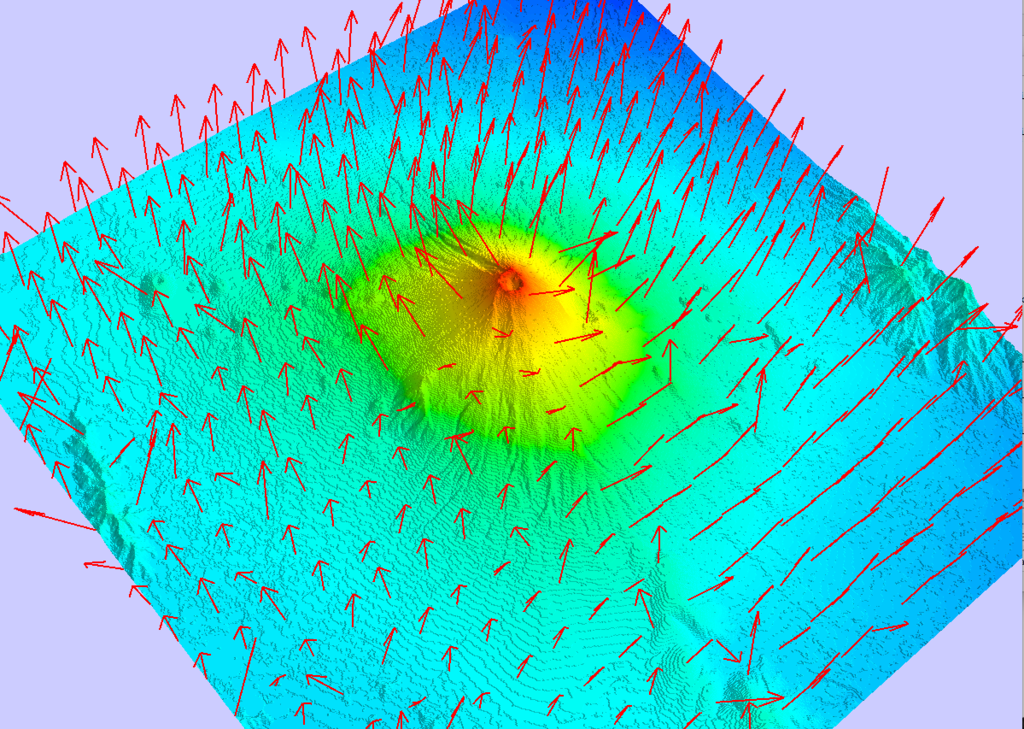
これを、大雑把に各点に垂直な法線ベクトルと見なせば、そんなに難しくもなく法線マップって作れるんじゃないということで、地球観測衛星「だいち」の標高データから富士山周辺の法線マップを作ってみたのが以下となります。

 

上の方法で求めた富士山周辺の法線ベクトルを図示すると大体こんな感じで

富士山の法線ベクトル

富士山の法線ベクトル

 

それを法線マップにしてみたのが以下で、さすが30m解像度の標高データ。

 

図を拡大してみると富士山の南山麓に、画像の左から右に、なにやら細い傷のような長い線が何本かクロスしているのがわかりますが、これ、何かなと思って衛星写真で調べてみたら、富士山の南山麓を取り囲むように張り巡らされた送電線の為に幅20〜30mほどぐらいの幅で延々と整地された土地で、要は周りの自然の地形と勾配の感じが違う、多分その部分だけ斜面方向には水平に近い感じで整地されている（？）ので、その部分が細長い線として法線マップ上に写っているのですね。

富士山の法線マップ

富士山の法線マップ

 

で、上の方法で作成した富士山周辺の法線マップをx3dで表示してみると、こんな感じで、物体の表面の法線（垂直）方向がわかれば、ライティングの視点からいえば、その面が光源から受け取る光の量がわかりますので（物体の真上に光源があればその物体の表面は最大限の光を受けますし、光源に対し斜めの面なら、当然、単位面積が受け取る光の量は減り、物体の表面に明暗の差が生まれますね。そこまで調べてませんが、多分、単純な行列計算で物体の表面の各部分が受ける光の量は計算できるのではないかな？）

 

本来真っ平らな立方体の表面が法線マップによるライティングの効果で地形に応じた凸凹があるように見えてますね。

 

なお、下の模型で使用している法線マップは、法線マップの効果がわかりやすいよ、上で作成した法線マップより勾配を３０倍ぐらいに誇張して作成した法線マップを使い表示しております。下のソースのdistx、distyの値を1として、標高メッシュ間の距離をわざと１メートルと仮定して作成したものです。

http://chamu.org/test/Fuji.html

ご覧の環境では、object要素がサポートされていないようです。外部文書を別ウィンドウで開いてください。

 

ということで、

上の法線マップを作成した時のソースは以下で

 

ALOSのデータの中身をみると、富士山周辺では、東西方向に25m間隔、南北方向に30m間隔のメッシュデータになっているようです。

  • ラスタサイズ 　= 3600 x 3600 x 1 
  • 左上経緯度 = 138.0, 36.0 
  • 解像度（X軸方向） = 0.000277777777778, 25.0454688384m 
  • 解像度（Y軸方向） = -0.000277777777778, 30.8219453463m 
  • 回転方向 = 0.0, 0.0 
  • データタイプ = Int16
#!/usr/bin/env python
# -*- coding: utf-8 -*- 


import numpy as np
from osgeo import gdal
from pyproj import *
from scipy import misc


raster_file = 'N035E138_AVE_DSM.tif'
dataset = gdal.Open(raster_file , gdal.GA_ReadOnly)

# データセット情報の取得
xsize = dataset.RasterXSize
ysize = dataset.RasterYSize

geotransform = dataset.GetGeoTransform()


# ラスターファイル左上経緯度付近でのXY方向の各ピクセル間の実際の距離を求める
g = Geod(ellps='WGS84')
az12,az21,distx = g.inv(geotransform[0], geotransform[3], geotransform[0]+geotransform[1], geotransform[3])
az12,az21,disty = g.inv(geotransform[0], geotransform[3], geotransform[0], geotransform[3]-geotransform[5])



# ラスタバンドをフェッチする
band = dataset.GetRasterBand(1)
dataType = band.DataType
dataTypeName = gdal.GetDataTypeName(dataType)


# ALOSのデーター概要をプリント
print("ラスタサイズ 　= {} x {} x {}".format(xsize,
                                    ysize,
                                    dataset.RasterCount))
print("左上経緯度       = {}, {}".format(geotransform[0], geotransform[3]))
print("解像度（X軸方向） = {}, {}m".format(geotransform[1], distx))
print("解像度（Y軸方向） = {}, {}m".format(geotransform[5], disty))
print("回転方向         = {}, {}".format(geotransform[2], geotransform[4]))
print("データタイプ = {}".format(dataTypeName))

# ラスタデータ取得
Raster = band.ReadAsArray(0, 0, xsize, ysize).astype(np.int16)


X, Y = np.meshgrid(np.linspace(0, band.XSize-1, band.XSize), np.linspace(0, band.YSize-1, band.YSize))

# 富士山周辺の標高データだけ取り出す
Z = Raster[1800:2800, 2000:3200]
X = X[1800:2800, 2000:3200]
Y = Y[1800:2800, 2000:3200]


# 法線マップを作成する

# X方向、Y方向の勾配を求める
Zy, Zx = np.gradient(Z)  

# X方向の勾配がZxということは、X方向にdistxメートル進んだ時に
# 標高がZx上がる（下がる）坂だと言ってるんだから各地点のX方向のベクトルは
gradx = np.dstack((np.ones_like(Zx)*distx, np.zeros_like(Zx), Zx))

# Y方向の勾配がZyということは、Y方向にdistyメートル進んだ時に
# 標高がZy上がる（下がる）坂だと言ってるんだから各地点のY方向のベクトルは
grady = np.dstack((np.zeros_like(Zy), np.ones_like(Zy)*disty, Zy))

# １点の２方向のベクトルがわかればその地点の坂に接する平面が求まり、
# そのベクトルのクロス積はその平面に垂直な法線ベクトルなのだから
normal = np.cross(gradx, grady)


# データを画像として保存するために、法線ベクトルのノルム（長さ） を1とする単位法線ベクトルに変換する
n = np.linalg.norm(normal, axis=2)
normal[:, :, 0] /= n
normal[:, :, 1] /= n
normal[:, :, 2] /= n

# 法線マップのデータ格納のお決まりに従い、単位法線ベクトルのX,Y,Zの各値を0～1.0 （中心0.5）の範囲に正規化してそれぞれの値をRGB値として格納
normal += 1
normal /= 2

misc.imsave('Fuji.jpg', normal)

  

 

因みに、上の考え方を流用して、

画像の隣同士の各ピクセル間のRGB値の値の差を標高差と同じように考えれば、Python使いにはおなじみレナさんの画像も

f:id:memomemokun:20190120233612p:plain

 

こんな感じに出来ますよね。

Python使いにはおなじみレナさんの画像の法線マップ

Python使いにはおなじみレナさんの画像の法線マップ

 

http://chamu.org/test/lena_normal.html

ご覧の環境では、object要素がサポートされていないようです。外部文書を別ウィンドウで開いてください。

 

画像を読み込んでみた時のソースは以下

#!/usr/bin/env python
# -*- coding: utf-8 -*- 

import numpy as np
from scipy import misc

img = misc.imread('lena_square.png')

# https://en.wikipedia.org/wiki/Grayscale#Converting_color_to_grayscale
# 標準的なカラーテレビや映像システムで用いられるYUVやそれに似た色空間における画像ののluma(Y')は以下としてイメージをグレースケール化
# Y=0.299R+0.587G+0.114B
Z=np.dot(img[...,:3], [0.299, 0.587, 0.114])

# 法線マップを作成する
Z = Z.astype("float64")

# X方向、Y方向の勾配を求める
Zy, Zx = np.gradient(Z)  

gradx = np.dstack((np.ones_like(Zx), np.zeros_like(Zx), Zx))
grady = np.dstack((np.zeros_like(Zy), np.ones_like(Zy), Zy))

normal = np.cross(gradx, grady)

# 法線ベクトルのノルム（長さ） を1とする単位法線ベクトルを求める
n = np.linalg.norm(normal, axis=2)
normal[:, :, 0] /= n
normal[:, :, 1] /= n
normal[:, :, 2] /= n

normal += 1
normal /= 2

misc.imsave('lena_normal.jpg', normal)